分布荷重の合力
このページでは、等分布荷重・三角形分布荷重・台形分布荷重の合力を解説します。
等分布荷重の合力
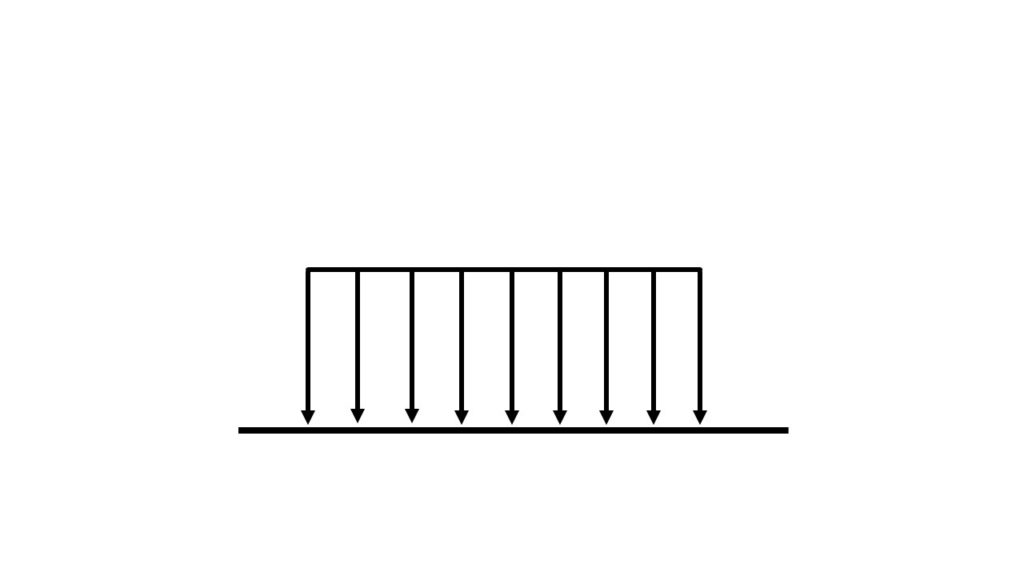
等分布荷重は↑図の通りの分布荷重です。分布荷重は”w [N/m]”のように与えられます。この分布荷重の合力は、分布荷重の長さ”ℓ [m]”をかけて、”w・ℓ [N]“となります。各矢印の長さを”w”、分布荷重の長さを”ℓ”とすると、長方形の面積を求めると”w・ℓ”となります。分布荷重の合力は面積を求めることと同じと考えるとわかりやすいでしょうか。
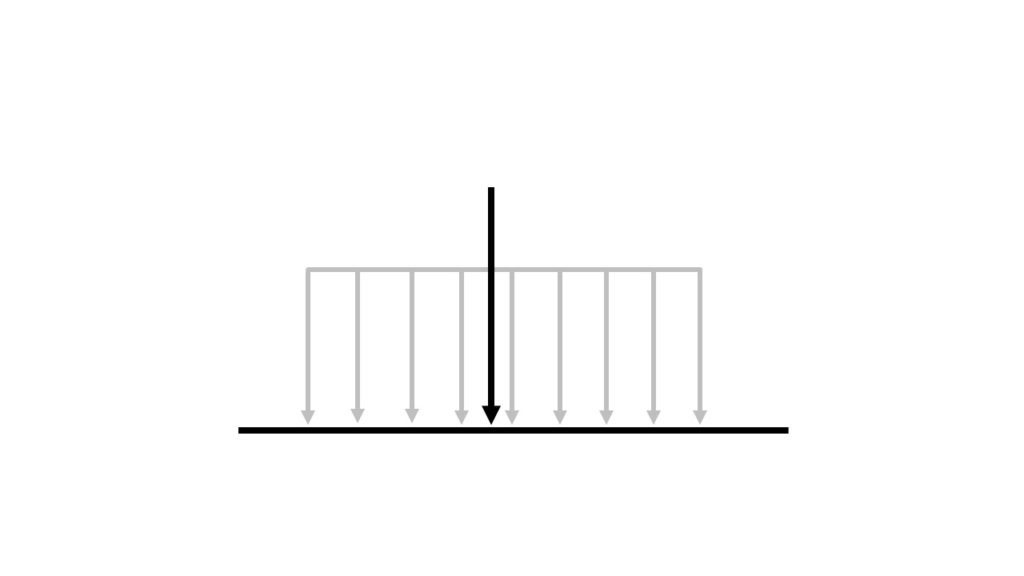
次に合力がかかる点を考えていきます。合力は長方形の重心にかかります。等分布荷重の場合では、↑図のようにℓ/2の部分(真ん中)になります。
三角形分布荷重の合力
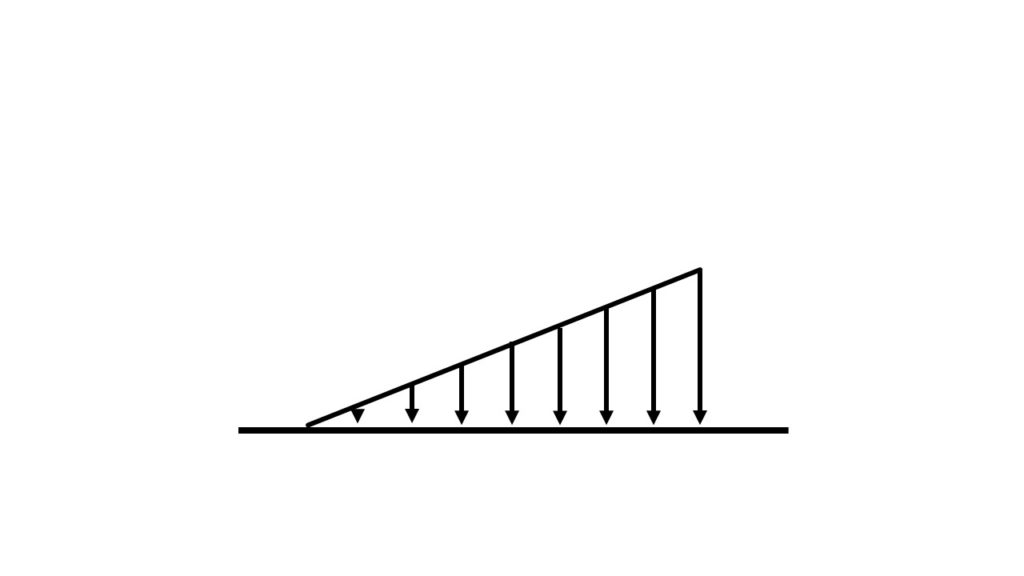
三角形分布荷重は↑図の通りです。分布荷重は”一番大きな部分(一番矢印が長い部分)がw [N/m]”のように与えられます。三角形の面積と同じように”Wℓ/2“で求められます。
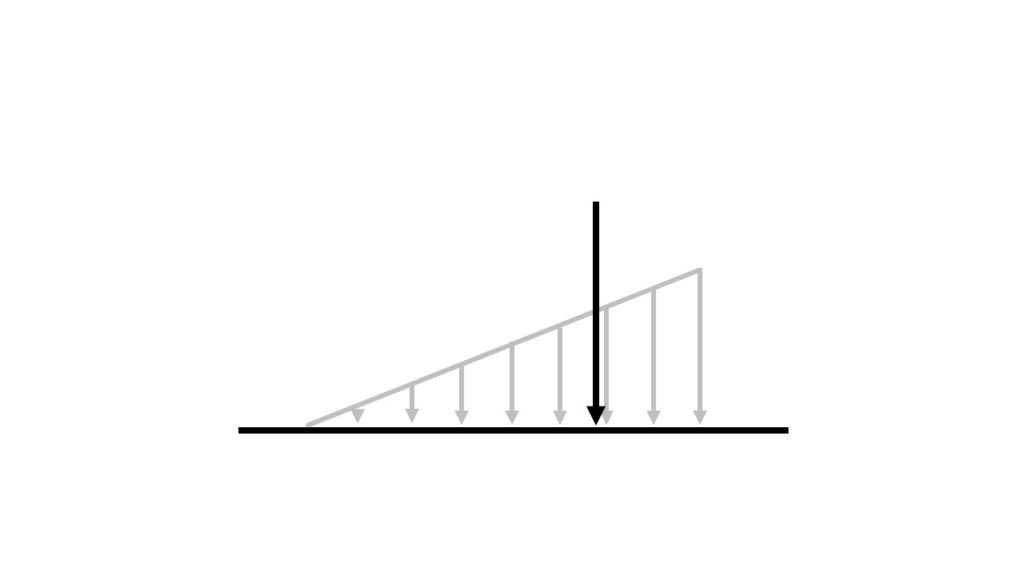
次に合力がかかる点を考えていきます。合力は三角形の重心にかかります。↑図の場合では、右から”ℓ/3“の部分になります。
台形分布荷重の合力
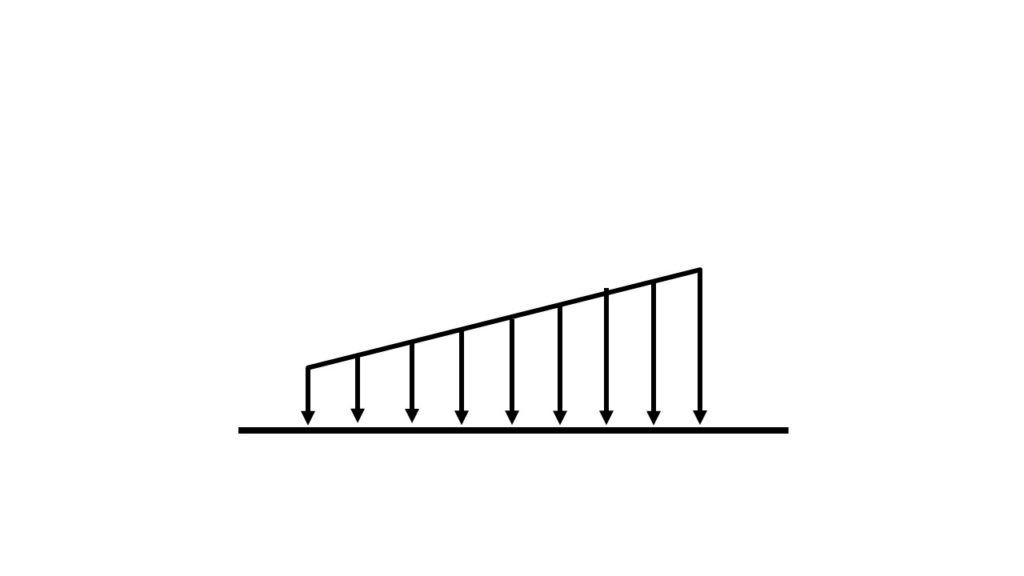
台形分布荷重は↑図の通りです。一番大きな荷重を”w1“、一番小さな荷重を”w2“とすると、合力は”(w1+W2)ℓ/2“で求められます。台形の面積公式と全く同じですね。

次にかかる点を考えていきます。合力は台形の重心にかかります。台形の重心は、台形を2つの三角形に分割し、その2つの三角形の重心を面積比で内分した点です。